In other words, we’re looking to calculate something along the lines of this: d ( mean 1) ( mean 2) std dev d ( mean 1) ( mean 2) std dev. r 0.50 (large effect): the effect accounts for 25 of the variance. In that context, a natural way of defining the effect size is to divide the difference between the means by an estimate of the standard deviation.
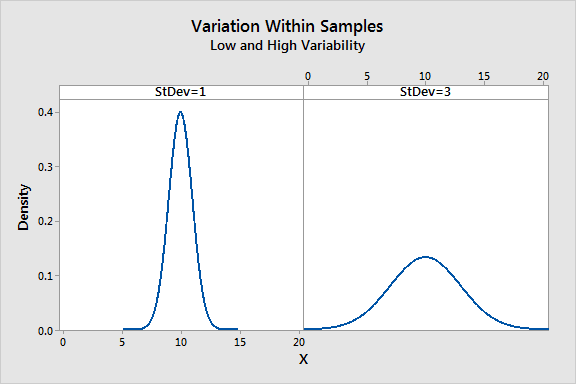
This indicates a ‘medium’ size difference: by convention, differences of 0.2, 0.5, and 0. Expressed in standard deviations, the group difference is 0.5: mean difference/standard deviation 5/10. Standardized effect sizes are useful when effects expressed in different units need to be combined or compared (Cumming 2014), e.g., a metaanalysis of a. The question that we have to ask ourselves is, what does these partial η 2 values actually mean? The way I generally interpret the partial η 2 for the main effect of Factor A is to interpret it as a statement about a hypothetical experiment in which only Factor A was being varied. there is no effect, and a value of 1 means that there is a perfect effect. Suppose, the standard deviation of exam scores is about 10 points in both groups.